Introduction to Variational Calculus

(മാസ്സ് ഇല്ലാത്ത പ്രകാശം ബ്ലാക്ക് ഹോളിൻറെ അകത്തേക്ക് പോകുന്നത് എങ്ങനെയാണെന്ന് സംശയം ഉള്ളവർ ഇത് ഒന്ന് നോക്കൂ.)

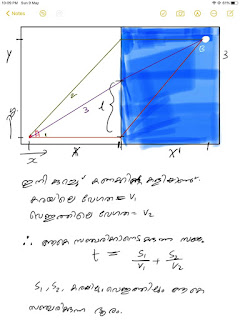
നിങ്ങൾ  A എന്ന പോയിന്റിൽ നിൽക്കുകയാണ്. നീല നിരത്തിലുള്ളത് വെള്ളമാണെന്നു കരുതുക. ഒരാൾ വെള്ളത്തിൽ മുങ്ങിക്കൊണ്ടിരിക്കുന്നു. അയാളെ രക്ഷിക്കണം. അതിനായി എത്രയും പെട്ടന്ന് അയാളുടെ അടുത്ത് എത്തണം. അതിനായി ഏതു വഴിയിലൂടെയാണീ പോകേണ്ടത്? എങ്ങനെ പോയാലാണ് ഏറ്റവും കുറഞ്ഞ സമയത്തു B യിൽ എത്താനാവുക?

കരയിൽ ഓടുന്നതിനേക്കാൾ കുറഞ്ഞ വേഗത്തിലേ വെള്ളത്തിൽ നീന്താനാകൂ. കരയിലെയും വെള്ളത്തിലേക്കു, വേഗതകൾ തന്നിട്ടുണ്ട് എന്ന് കരുതുക. ഇവിടെ സാധ്യമായ ചില പാതകൾ നമുക്ക് പരിഗണിക്കാം. (ചിത്രം നോക്കുക)

ഇനി ഉറച്ചു കണക്കിന്റെ കളിയാണ്.

കരയിലെ വേഗത =v1.
വെള്ളത്തിലെ വേഗത =v2

Therefore, total time t=s1/v1+s2/v2.

s1,s2 കരയിലും വെള്ളത്തിലും സഞ്ചരിക്കുന്ന ദൂരം.

ഇനിയുള്ളത് കുറച്ചു ബുദ്ധിമുട്ടായിരിക്കും .

ഓരോ പാതയിലൂടെയുമുള്ള സഞ്ചാരം നമുക്കൊന്ന് ആലോചിച്ചു നോക്കാം.

1. കരയിലൂടെ ഓടുമ്പോൾ x ഇന്റെ  വാല്യൂ മാത്രമേ മാറുന്നുള്ളു. y യുടെ സ്ഥാനം മാറുന്നില്ല. വെള്ളത്തിലെത്തിക്കഴിഞ്ഞു മാത്രമാണ് y മാറാൻ തുടങ്ങുന്നത്.

അതായത് അരയിലായിരുന്നപ്പോൾ സഞ്ചരിച്ച ദൂരം = X ( ചിത്രം നോക്കുക )

വെള്ളത്തിൽ സഞ്ചരിച്ച ദൂരം =( ചിത്രം നോക്കുക )

സമയം ചിത്രത്തിൽ എഴുതിയിട്ടുണ്ട് (നമ്പർ 5)

2. ഈ പാതയിലൂടെ സഞ്ചരിക്കുമ്പോ വെള്ളത്തിൽ വച്ച് y ക്കു മാറ്റമൊന്നും ഇല്ല. x മാത്രമേ മാറുന്നുള്ളു. മുന്നത്തെതിന്റെ നേരെ തിരിച്ചുള്ള ഒരു സാഹചര്യമാണ് ഇത്. (സമവാക്യങ്ങൾക്കു ചിത്രം നോക്കുക) സമയം t2.

3. ഈ പാതയിൽ x നും  y  ക്കും മാറ്റമുണ്ട്. ഇവിടെ സമയം t3.

ഇനി ഓരോന്നിനും ഓരോ മൂല്യങ്ങൾ ഇട്ടുകൊടുത്തുനോക്കാം.

X= 1 m.

Y= 1 m

X'= 1 m
v1= 2 m/s
v2=1m/s

l അവിടെ നിൽക്കട്ടെ.

കണക്കുകൂട്ടുമ്പോൾ കിട്ടുന്നത്

t1= 1.9 s

t2= 1.7 s

l ന്റെ മൂല്യം എന്തായാലും 0 നും 1 നും ടേക്ക് ആയിരിക്കും. തത്കാലത്തേക്ക് ഞാൻ എടുക്കുന്നു l=.5.

ഇത് വച്ച് കിട്ടുന്നത് t3=1.675 s.

 
l ന്റെ മൂല്യം മാറ്റിയാൽ ചിലപ്പോൾ ഇതിലും കുറഞ്ഞ മൂല്യങ്ങൾ കിട്ടുമായിരിക്കും,. കൃത്യമായി ഏതാണെന്നു കണ്ടുപിടിക്കാനും വഴിയുണ്ട്. അതാണ് Calculus.

അതുപയോഗിച്ചു കിട്ടുന്നത്  l=0.700

So, t3=1.654 s.

അതയായതു ഇന്റിനു മുമ്പ് കണക്കുകൂട്ടിയതിനേക്കാൾ ഇവിടെ സമയം കുറവാണ്. അപ്പോൾ പാത ഏകദേശം മൂന്നാമത്തെ പാത പോലെ തന്നെ ഉണ്ടാകും. ഇനി ഇതിന്റെ ചില ഉപയോഗങ്ങൾ നോക്കാം.

1. മുകളിൽ പാതകൾ അടയാളപ്പെടുത്തിയ ചിത്രത്തിൽ മൂന്നാമത്തെ പാത എവിടെയെങ്കിലും കണ്ടിട്ടുള്ളതാണ് തോന്നിയോ ? അതെ, സ്കൂളിൽ പഠിച്ചിട്ടുള്ള അപവർത്തത്തിന്റെ ചിത്രമാണ് അത്. പ്രകാശം എപ്പോഴും  സഞ്ചരിക്കുന്ന പാത അത് ഒരു പോയിന്റിൽ നിന്നും വേറൊരു പോയിന്റിലേക്കു സഞ്ചരിക്കാൻ ഏറ്റവും കുറഞ്ഞ സമയം എടുക്കുന്നത് ഏതു പാതയിലാണോ ആ പാത ആയിരിക്കും, അപവർത്തനം അഥവാ refrachion നു ലാറണം ഇത് തന്നെ ആണ്. ഈ തത്വത്തെ Fermath's principle എന്ന് വിളിക്കുന്നു.  

ഗുരുത്വാകര്ഷണത്തിന്റെ സ്വാധീനം മൂലം മാസ്സ് ഇല്ലാത്ത പ്രകാശം എങ്ങനെ വളയും എന്ന സംശയം ഉള്ളവർക്ക് അതിന്റെ ഉത്തരം കിട്ടിക്കാണും എന്ന് കരുതുന്നു.

2.  ഒരു സ്പേസിൽ രണ്ടു പോയിന്റുകൾ തമ്മിലുള്ള ഏറ്റവും ദൂരം കുറഞ്ഞ പാത ഏതാണെന്നു  ഈ സൂത്രം ഉപയോഗിച്ച്  കണ്ടുപിടിക്കാം. ഒരു plane ൽ അത് നേരേഖ ആയിരിക്കും. ഒരു ഗോളത്തിനു പുറത്തോ മറ്റോ ആണെങ്കിൽ വളഞ്ഞ വര ആയിരിക്കും.

3. ഇങ്ങനെ ഏതെങ്കിലും functional നെ minimize ചെയ്യാൻ ഉപയോഗിക്കുന്ന ഗണിതത്തിലെ ഒരു ടൂൾ ആണ് Variational Calculus.

4. Classical Mechancs ൽ ഉപയോഗിക്കുന്ന ഏറ്റവും ശക്തമായ ടൂൾ ആണ് Variational Calculus. ഇതിൽ സമയം അല്ല, Action എന്നൊരു സംഭവം ആണ് കുറക്കാൻ ശ്രമിക്കുന്നത്. ( നമ്മളല്ല, പ്രകൃതി.) ഇതിനെ വിളിക്കുന്ന പേരാണ് Hamilton's Principle of Least Action.

Referenes:

1. Optics by Brijlal
2. Feynman Lectures
3. Classical Mechanics by Goldstein
4. Theoretical Mechanics Lectures by Prof Charubhatt Khadolkar, IIT Guwahathi.
5. Classical Mechanics Lectures by Susskind.